Week 3

Logistic population growth and stability analysis

Lecture in a nutshell

  • Model derivation:
    1. Population growth rate: \(Birth - Death + Immigration - Emigration\)
    2. Per capita growth rate: \((birth - death + immigration - emigration)\times N\).

  • Assumptions:
    1. Closed population: \(Immigration\) = \(Emigration = 0\)
    2. All individuals are identical: no genetic/age/stage structure
    3. Continuous population growth without time lag
    4. Per capita birth and death rates are time-independent BUT density-dependent
    5. Resource is limited: negative density-dependence (NDD) \(\frac{dr_{(N)}}{dt} < 0\)
    6. Linear density-dependence: \(b_{(n)} = b_{0}-b_{N}N\); \(d_{(n)} = d_{0}+d_{N}N\) \(\begin{aligned}\frac{dN}{dt}&=(b_{0}-b_{N}N-d_{0}-d_{N}N)N\\&=((b_{0}-d_{0})-(d_{N}+b_{N})N)N\\&=(r_{0}-\alpha N)N\\&=r_{0}N(1-\frac{N}{K})\end{aligned}\)

  • Integration of the differential equation
    1. \(N_{(t)} = \frac{K}{1-\frac{N_{0}-K}{N_{0}}e^{-r_{0}t}}\)
    2. Equilibrium \(N^*\): good candidates where the system will end up
    3. \(\frac{dN}{dt} = f_{(N^*)} = r_{0}N^{*}(1-\frac{N^*}{K}) = 0\); \(N^* = 0, K\)
    4. Attracting (Stable) vs. Repelling (Unstable) vs. Saddle

  • Graphical analysis
    1. Plot the function \(\frac{dN}{dt} = f(N)\) and determine the direction of change (positive/negative) on both sides of the equilibrium points \(N^*\)

  • Local stability analysis
    1. A small “displacement” from the equilibrium: \(\epsilon_{(t)} = N - N^*\)
    2. Examine how \(\epsilon_{(t)}\) changes over time (i.e., the behavior of the small displacement): \(\frac{d\epsilon_{(t)}}{dt} = f(N-N^*) = f(N^*) + \epsilon \frac{dN}{dt}|_{N = N^*} + O_{(\epsilon^2)} \approx \epsilon\frac{dN}{dt}|_{N = N^*} = \lambda \epsilon\); \(\epsilon_{(t)} = \epsilon_{0}e^{\lambda t}\)
      (the behavior of \(\epsilon_{(t)}\) is determined by the sign of \(\lambda\))
    3. General procedure: take derivative of the differential equation with respect to \(N\) and evaluate it at the equilibrium point \(N^*\):
      • \(\frac{dN}{dt}|_{N = N^*} = \lambda > 0\): unstable equilibrium
      • \(\frac{dN}{dt}|_{N = N^*} = \lambda < 0\): stable equilibrium


Lab demonstration

In this lab, we will solve the differential equation for logistic population growth and visualize how the population sizes change over time. Have a quick review of the lab section in Week 2.

We will also take a look at how population growth rate (\(\frac{dN}{dt}\)) and per capita growth rate (\(\frac{dN}{dtN}\)) change with population size (\(N\)).

Part 1 - Solving the logistic growth equation and visualize the results

library(tidyverse)
library(deSolve)

### Model specification
logistic_model <- function(times, state, parms) {
  with(as.list(c(state, parms)), {
    dN_dt = r*N*(K-N)/K  # logistic growth equation
    return(list(c(dN_dt)))  # return the results  
  })
}

### Model application
times <- seq(0, 10, by = 0.1)  # time steps to integrate over
state <- c(N = 10)  # initial population size
parms <- c(r = 1.5, K = 500)  # intrinsic growth rate and carrying capacity

# run the ode solver
pop_size <- ode(func = logistic_model, times = times, y = state, parms = parms)

### Visualize the results
ggplot(data = as.data.frame(pop_size), aes(x = time, y = N)) + 
  geom_point() + 
  labs(title = paste0("Logistic Growth \n (r = ", parms["r"], ", K = ", parms["K"], ")")) +
  theme_classic(base_size = 12) + 
  theme(plot.title = element_text(hjust = 0.5)) +
  scale_x_continuous(limits = c(0, 10.5), expand = c(0, 0)) +
  scale_y_continuous(limits = c(0, max(as.data.frame(pop_size)$N)*1.1), expand = c(0, 0))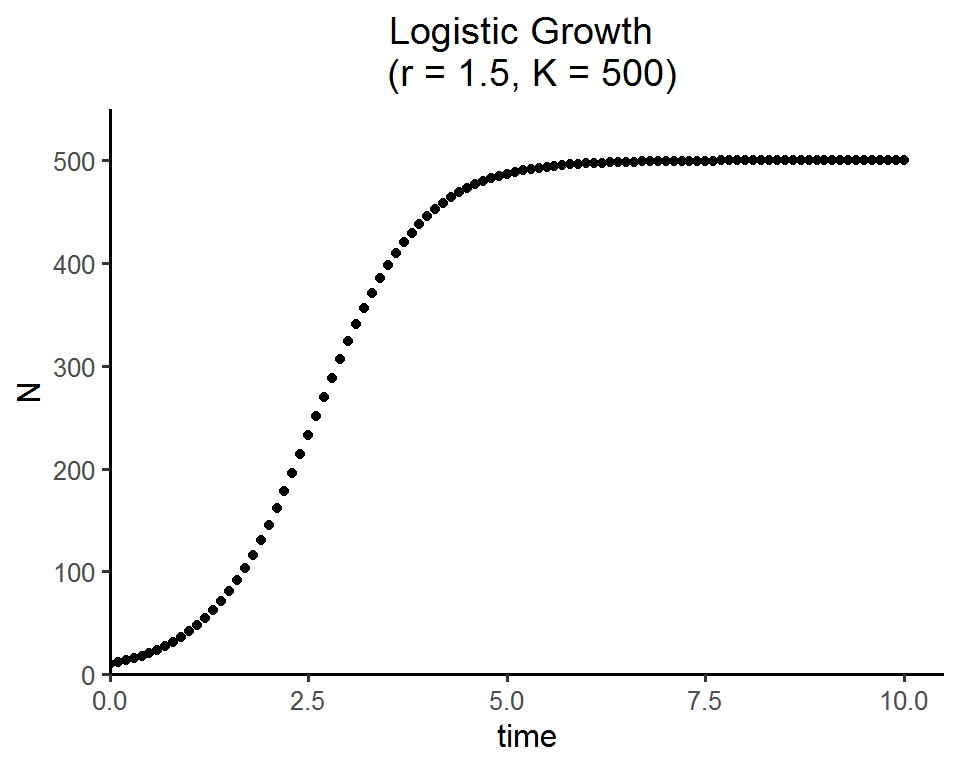


Here is an interactive web app for the logistic growth model. Feel free to play around with the parameters/values and see how the population trajectories change. Please select a set of parameters of your choice and reproduce the output figure you see in this app.


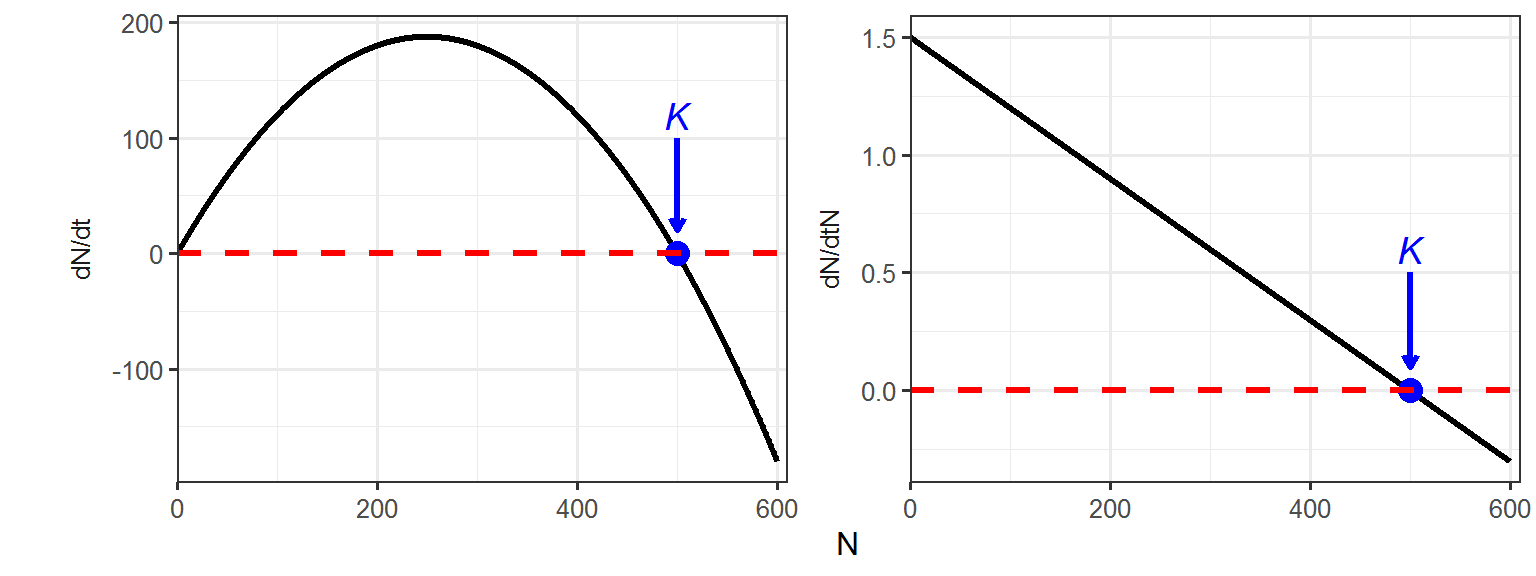
Part 2 - The relationship between population growth rate (\(\frac{dN}{dt}\))/per capita growth rate (\(\frac{dN}{dtN}\)) and population size (\(N\))

# parameters
r <- 1.5
K <- 500

# a vector of population sizes
N <- 0:600

# calculate the population growth rates and per capita growth rates
dN_dt <- r*N*(K-N)/K 
dN_dtN <- r*(K-N)/K

# organize into a dataframe
logistic_data <- data.frame(N, dN_dt, dN_dtN) %>%
  pivot_longer(cols = c(dN_dt, dN_dtN), 
               names_to = "vars", 
               values_to = "values")

# plot 
K_df <- data.frame(xend = c(500, 500),
                   yend = c(20, 0.1),
                   xstart = c(500, 500),
                   ystart = c(100, 0.5),
                   labels = c("italic(K)", "italic(K)"),
                   vars = c("dN_dt", "dN_dtN"))

ggplot(data = logistic_data, aes(x = N, y = values)) + 
  geom_line(size = 1.2) + 
  geom_point(x = 500, y = 0, size = 4, color = "blue") +
  geom_hline(yintercept = 0, linetype = "dashed", color = "red", size = 1.2) +
  labs(x = "N", y = "") +
  facet_wrap(~vars, 
             ncol = 2, 
             scales = "free_y",
             strip.position = "left", 
             labeller = as_labeller(c(dN_dt = "dN/dt", 
                                      dN_dtN = "dN/dtN"))) + 
  theme_bw(base_size = 12) +
  theme(strip.background = element_blank(),
        strip.placement = "outside",
        legend.position = "top",
        legend.title = element_blank()) + 
  scale_x_continuous(limits = c(0, 610), expand = c(0, 0)) + 
  geom_segment(data = K_df, 
               aes(x = xstart, y = ystart, xend = xend, yend = yend), 
               arrow = arrow(length = unit(0.03, "npc")), 
               size = 1.2,
               color = "blue") + 
  geom_text(data = K_df, 
            aes(x = xstart, y = ystart*1.2, label = labels),
            size = 5, 
            color = "blue",
            parse = T)


Additional readings

Logistic Growth